Unterschied zwischen absoluter und relativer Fehler | Absoluter Fehler vs. Relativer Fehler
Schlüsselunterschied - absoluter Fehler vs relativer Fehler
Absoluter Fehler und relativer Fehler sind zwei Möglichkeiten zur Anzeige Fehler in experimentellen Messungen, obwohl zwischen absoluter Abweichung und relativer Abweichung aufgrund ihrer Berechnung ein Unterschied besteht. Die meisten Messungen in wissenschaftlichen Experimenten beinhalten Fehler aufgrund von Instrumentenfehlern und menschlichen Fehlern. In einigen Fällen gibt es für ein bestimmtes Messgerät einen vordefinierten konstanten Wert für den absoluten Fehler (der kleinste Wert zB: - Lineal = +/- 1 mm) Es ist der Unterschied zwischen true Wert und den experimentellen Wert. Der relative Fehler hängt jedoch vom experimentellen Wert und vom absoluten Fehler ab. Sie wird bestimmt, indem das Verhältnis des absoluten Fehlers und des experimentellen Wertes genommen wird. Somit ist die -Tastendifferenz zwischen dem absoluten Fehler und dem relativen Fehler, der absolute Fehler ist die Größe des Unterschieds zwischen dem genauen Wert und der Näherung Der relative Fehler wird berechnet, indem der absolute Fehler durch die Größe des exakten Werts dividiert wird. Was ist absoluter Fehler?
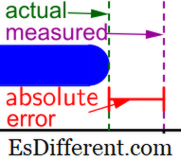
Absoluter Fehler ist ein Hinweis auf die Unsicherheit einer Messung. Mit anderen Worten, es misst, in welchem Ausmaß der wahre Wert von seinem experimentellen Wert abweichen kann. Der absolute Fehler wird in denselben Einheiten ausgedrückt wie die Messung.Beispiel:
Stellen Sie sich vor, Sie möchten die Länge eines Bleistifts mit einem Lineal mit Millimetermarkierungen messen. Wir können seine Länge auf den nächsten Millimeterwert messen. Wenn Sie einen Wert von 125 mm erhalten, wird dies als 125 +/- 1 mm angegeben. Der absolute Fehler beträgt +/- 1 mm.
Relativer Fehler einer Monte-Carlo-Integration zur Berechnung von pi
Was ist der Unterschied zwischen Absolut- und Relativfehler?
Definition des absoluten Fehlers und des relativen Fehlers
Absoluter Fehler:
Absoluter Fehler ist ein Δx-Wert (+ oder - Wert), wobei x eine Variable ist; es ist der physikalische Fehler einer Messung.Es ist auch bekannt als der tatsächliche Fehler in einer Messung.
Mit anderen Worten, es ist der Unterschied zwischen dem wahren Wert und dem experimentellen Wert.
- diff Artikel Mitte vor Tabelle ->
Absoluter Fehler = Istwert - Messwert
Relativer Fehler:
Relativer Fehler ist das Verhältnis von Absolutfehler (Δx) zum Messwert (x). Sie wird entweder als Prozentsatz (prozentualer Fehler) oder als Bruch (Bruchteilsunsicherheit) ausgedrückt. |
Einheiten und Berechnung des absoluten Fehlers und des relativen Fehlers
Einheiten

Absoluter Fehler:
Es hat die gleichen Einheiten wie der gemessene Wert. Wenn Sie zum Beispiel die Länge eines Buches in Zentimetern (cm) messen, hat der absolute Fehler auch die gleichen Einheiten.
Relativer Fehler:
Relativer Fehler kann als Bruch oder als Prozentsatz ausgedrückt werden. Beide haben jedoch keine Einheit im Wert.
Fehlerberechnung
Beispiel 1:
Die tatsächliche Länge eines Landes beträgt 500 Fuß. Ein Messinstrument zeigt die Länge von 508 Fuß an.
| Absoluter Fehler: Absoluter Fehler = [Aktueller Wert - Messwert] = [508-500] Fuß = 8 Fuß |
Relativer Fehler:
In Prozent:
Beispiel 2:
Ein Student wollte die Höhe einer Wand in einem Raum messen. Er maß den Wert mit einem Meter Lineal (mit Millimeterwerten), es war 3. 215m.

Absoluter Fehler:

Absoluter Fehler = +/- 1 mm = +/- 0. 001m
| (Der kleinste Messwert, der mit dem Lineal gelesen werden kann) |
Relativer Fehler:
Relativer Fehler = Absoluter Fehler ÷ Experimenteller Wert = 0. 001 m ÷ 3. 215 m * 100 = 0. 0003% Bild Courtesy: "Absoluter Fehler" von DEMcAdams - Eigene Arbeit. (CC BY-SA 4. 0) über Wikimedia Commons "Relativer Fehler einer Monte-Carlo-Integration zur Berechnung von pi" von Jorgecarleitao - Python und Xmgrace. (CC BY-SA 3. 0) über Wikipedia