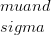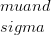Binomial vs. Normalverteilung
Wahrscheinlichkeitsverteilungen zufälliger Variablen spielen eine wichtige Rolle im Bereich der Statistik. Von diesen Wahrscheinlichkeitsverteilungen sind Binomialverteilung und Normalverteilung zwei der am häufigsten auftretenden im realen Leben.
Was ist Binomialverteilung?
Binomialverteilung ist die Wahrscheinlichkeitsverteilung entsprechend der Zufallsvariablen X, die Anzahl der Erfolge einer endlichen Folge unabhängiger Ja / Nein-Experimente, die jeweils eine Wahrscheinlichkeit haben des Erfolgs p. Aus der Definition von X, ist ersichtlich, dass es sich um eine diskrete Zufallsvariable handelt; daher ist auch die Binomialverteilung diskret.
-

Die Verteilung wird als < n ist die Anzahl der Experimente und p ist die Erfolgswahrscheinlichkeit. Nach der Wahrscheinlichkeitstheorie können wir folgern, dass B (n, p) der Wahrscheinlichkeits-Massenfunktion folgt. Aus dieser Gleichung kann weiter abgeleitet werden, dass der Erwartungswert von X

, E (X) = np und die Varianz von X, V (X) = np (1- p).
Betrachten Sie zum Beispiel ein zufälliges Experiment, bei dem eine Münze dreimal geworfen wird. Definiere den Erfolg als den Erhalt von H, den Fehler als Erlangung von T und die Zufallsvariable X
als Anzahl der Erfolge im Experiment. Dann ist
X ~ B (3, 0,5) und die Wahrscheinlichkeitsmassenfunktion von X gegeben durch. Daher ist die Wahrscheinlichkeit, mindestens 2 H's zu erhalten, P (X ≥ 2) = P (X

= 2 oder X < (X = 2) + P (X = 3) = 3 C 2 (0,5 2 (0, 5 1
) + 3
>) = 0. 375 + 0. 125 = 0. 5.
Was ist Normalverteilung? Normalverteilung ist die durch die Wahrscheinlichkeitsdichtefunktion definierte kontinuierliche Wahrscheinlichkeitsverteilung,
. Die Parameter bezeichnen den Mittelwert und die Standardabweichung der interessierenden Population. Bei
wird die Verteilung als Standardnormalverteilung bezeichnet. Diese Verteilung wird normal genannt, da die meisten natürlichen Phänomene der Normalverteilung folgen. Zum Beispiel ist der IQ der menschlichen Bevölkerung normalerweise verteilt. Wie aus dem Graphen ersichtlich ist, ist es unimodal, symmetrisch um den Mittelwert und glockenförmig. Mittelwert, Modus und Median stimmen überein. Die Fläche unter der Kurve entspricht dem Teil der Bevölkerung, der eine gegebene Bedingung erfüllt.
Die Bevölkerungsteile im Intervall , , sind ungefähr 68.2%, 95,6% bzw. 99,8%.
Was ist der Unterschied zwischen binomischen und normalen Verteilungen?
Binomialverteilung ist eine diskrete Wahrscheinlichkeitsverteilung, während die Normalverteilung eine kontinuierliche ist.
Die Wahrscheinlichkeits-Massenfunktion der Binomialverteilung ist , während die Wahrscheinlichkeitsdichtefunktion der Normalverteilung

ist. Die Binomialverteilung wird unter bestimmten Bedingungen mit Normalverteilung approximiert, nicht umgekehrt.