Unterschied zwischen Tangentialbeschleunigung und Centripetalbeschleunigung: Tangentialbeschleunigung gegenüber Centripetalbeschleunigung

Tangentialbeschleunigung gegenüber Centripetalbeschleunigung

Beschleunigung ist die Geschwindigkeitsänderung der Geschwindigkeit, und wenn sie mit dem Kalkül ausgedrückt wird, ist dies die zeitliche Ableitung der Geschwindigkeit. Die Tangentialbeschleunigung und die Zentripetalbeschleunigung sind Komponenten der Beschleunigung für ein Teilchen oder einen starren Körper in einer Kreisbewegung.

Tangentiale Beschleunigung

Betrachten Sie ein Partikel, das sich entlang eines Pfads bewegt, wie im Diagramm gezeigt. Im betrachteten Fall befindet sich das Teilchen in einer Winkelbewegung, und die Geschwindigkeit des Teilchens ist tangential zum Weg.

Die Änderungsgeschwindigkeit der Tangentialgeschwindigkeit ist als Tangentialbeschleunigung definiert und wird mit a _t bezeichnet.

t

dv _t / dt _{Dies berücksichtigt jedoch nicht die Gesamtbeschleunigung des Teilchens. Nach Newtons erstem Gesetz muss, da ein Teilchen vom geradlinigen Weg und von der Wende abweicht, eine andere Kraft vorhanden sein; Daher können wir folgern, dass es eine Beschleunigungskomponente geben muss, die senkrecht zur Tangentialbeschleunigungskomponente gerichtet ist, d. e. zum Punkt O in der gezeigten Instanz. Diese Beschleunigungskomponente ist als} normale Beschleunigung

bekannt und wird mit a n bezeichnet. t

/ > u

n sind die Einheitsvektoren in tangentialer und normaler Richtung, so kann die resultierende Beschleunigung durch folgenden Ausdruck gegeben werden. & Lt; 999 & gt; 999 & gt; 999 & gt; 999 & gt; 999 & gt; 999 & gt; _t 2 / r) u _n Centripetallbeschleunigung

Beachten Sie nun, dass die die normale Beschleunigung induzierende Kraft konstant ist. In diesem Fall tritt das Teilchen in eine Kreisbahn mit einem Radius r ein. Dies ist ein Sonderfall der Winkelbewegung, und der Normalbeschleunigung wird der Begriff der Zentripetalbeschleunigung gegeben. Die Kraft, die die Kreisbewegung antreibt, wird als _{Zentripetalkraft} bezeichnet. _{Die Zentripetalbeschleunigung ist auch durch den obigen Ausdruck gegeben, aber Winkelbeziehungen in Geschwindigkeit und Beschleunigung können verwendet werden, um sie in Bezug auf die Winkelgeschwindigkeit zu geben.} Daher ist _a c _{= v} t ₂ / r = -rω ₂ (Negatives Vorzeichen zeigt an, die entgegengesetzte Richtung des Radiusvektors) _{Die Nettobeschleunigung kann durch die Resultante der beiden Komponenten a} ^c und a _t

erhalten werden.

Was ist der Unterschied zwischen Tangentialbeschleunigung und Centripetalbeschleunigung? • Tangential- und Zentripetalbeschleunigungen sind zwei Komponenten der Beschleunigung eines Teilchens / Körpers in einer Kreisbewegung. • Die Tangentialbeschleunigung ist die Änderungsgeschwindigkeit der Tangentialgeschwindigkeit, und sie ist immer tangential zur Kreisbahn und normal zum Radiusvektor.

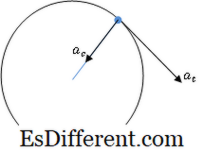
• Die Zentripetalbeschleunigung ist auf den Mittelpunkt des Kreises gerichtet, und diese Beschleunigungskomponente ist der Hauptfaktor, der das Teilchen in der Kreisbahn hält.

• Für ein Teilchen in einer Kreisbewegung liegt der Beschleunigungsvektor immer innerhalb der Kreisbahn.