Unterschied zwischen linearen und nichtlinearen Differentialgleichungen

Nichtlineare Differentialgleichungen

Eine Gleichung, die mindestens einen Differentialkoeffizienten oder eine Ableitung einer unbekannten Größe enthält, wird als Differentialgleichung bezeichnet. Eine Differentialgleichung kann entweder linear oder nichtlinear sein. Der Umfang dieses Artikels ist zu erklären, was ist eine lineare Differentialgleichung, was ist nichtlineare Differentialgleichung, und was ist der Unterschied zwischen linearen und nichtlinearen Differentialgleichungen.

Seit der Entwicklung der Analysis im 18. Jahrhundert durch Mathematiker wie Newton und Leibnitz hat die Differentialgleichung eine wichtige Rolle in der Geschichte der Mathematik gespielt. Differentialgleichungen sind aufgrund ihres Anwendungsbereichs in der Mathematik von großer Bedeutung. Differentialgleichungen stehen im Zentrum jedes Modells, das wir entwickeln, um jedes Szenario oder Ereignis auf der Welt zu erklären, unabhängig davon, ob es sich um Physik, Ingenieurwesen, Chemie, Statistik, Finanzanalyse oder Biologie handelt. In der Tat, bis der Kalkül eine etablierte Theorie wurde, waren geeignete mathematische Werkzeuge nicht verfügbar, um die interessanten Probleme in der Natur zu analysieren.

Resultierende Gleichungen aus einer bestimmten Anwendung von Kalkül können sehr komplex und manchmal nicht lösbar sein. Es gibt jedoch einige, die wir lösen können, die aber ähnlich und verwirrend aussehen können. Zur einfacheren Identifizierung werden daher Differentialgleichungen nach ihrem mathematischen Verhalten kategorisiert. Lineare und nichtlineare ist eine solche Kategorisierung. Es ist wichtig, den Unterschied zwischen linearen und nichtlinearen Differentialgleichungen zu identifizieren.

Was ist eine lineare Differentialgleichung?

Nehmen wir an, dass f: X → Y und f (x) = y eine 999 Differentialgleichung ohne nichtlineare Terme der unbekannten Funktion y ist als lineare Differentialgleichung bekannt. Es setzt die Bedingung voraus, dass y keine höheren Indexterme wie y

2 ^{, y} 3 ^{, … und Vielfache von Ableitungen wie} Begriffe wie Sin

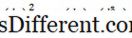
y, e y ^{^ - 2 oder ln} y. Es nimmt die Form an,

und

g sind Funktionen von x. Die Gleichung ist eine Differentialgleichung der Ordnung n, die der Index der Ableitung höchster Ordnung ist. In einer linearen Differentialgleichung ist der Differentialoperator ein linearer Operator, und die Lösungen bilden einen Vektorraum. Infolge der linearen Natur der Lösungsmenge ist eine lineare Kombination der Lösungen auch eine Lösung für die Differentialgleichung.Das heißt, wenn y 1

und y ₂ Lösungen der Differentialgleichung sind, 1 + C ₂ y 2 _{ist auch eine Lösung.}

_{Die Linearität der Gleichung ist nur ein Parameter der Klassifikation und kann weiter in homogene oder nicht homogene und gewöhnliche oder partielle Differentialgleichungen eingeteilt werden. Wenn die Funktion} g _{= 0 ist, ist die Gleichung eine lineare homogene Differentialgleichung. Ist} f _{eine Funktion von zwei oder mehr unabhängigen Variablen} (f: X, T → Y)

und

f (x, t) = y Gleichung ist eine lineare partielle Differentialgleichung.

Die Lösungsmethode für die Differentialgleichung ist abhängig vom Typ und den Koeffizienten der Differentialgleichung. Der einfachste Fall tritt auf, wenn die Koeffizienten konstant sind. Klassisches Beispiel für diesen Fall ist Newtons zweites Bewegungsgesetz und seine verschiedenen Anwendungen. Newtons zweites Gesetz erzeugt eine lineare Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten. Was ist eine nichtlineare Differentialgleichung? Gleichungen, die nichtlineare Terme enthalten, werden als nichtlineare Differentialgleichungen bezeichnet. Alle oben genannten sind nichtlineare Differentialgleichungen. Nichtlineare Differentialgleichungen sind schwer zu lösen, daher ist eine genaue Untersuchung erforderlich, um eine korrekte Lösung zu erhalten. Im Fall von partiellen Differentialgleichungen haben die meisten Gleichungen keine allgemeine Lösung. Daher muss jede Gleichung unabhängig behandelt werden. Navier-Stokes-Gleichung und Eulers Gleichung in der Strömungsdynamik sind Einsteins Feldgleichungen der allgemeinen Relativitätstheorie wohlbekannte nichtlineare partielle Differentialgleichungen. Manchmal kann die Anwendung der Lagrange-Gleichung auf ein variables System zu einem System nichtlinearer partieller Differentialgleichungen führen. Was ist der Unterschied zwischen linearen und nichtlinearen Differentialgleichungen?

• Eine Differentialgleichung, die nur die linearen Terme der unbekannten oder abhängigen Variablen und ihrer Ableitungen enthält, wird als lineare Differentialgleichung bezeichnet. Es hat keinen Term mit der abhängigen Variable des Index höher als 1 und enthalten kein Vielfaches seiner Derivate. Es kann keine nichtlinearen Funktionen wie trigonometrische Funktionen, Exponentialfunktion und logarithmische Funktionen in Bezug auf die abhängige Variable haben. Jede Differentialgleichung, die oben erwähnte Terme enthält, ist eine nichtlineare Differentialgleichung.

• Lösungen linearer Differentialgleichungen erzeugen Vektorraum und der Differentialoperator ist auch ein linearer Operator im Vektorraum.

• Lösungen linearer Differentialgleichungen sind relativ einfach und es gibt allgemeine Lösungen. Für nichtlineare Gleichungen existiert in den meisten Fällen die allgemeine Lösung nicht, und die Lösung kann problemspezifisch sein. Dies macht die Lösung viel schwieriger als die linearen Gleichungen.