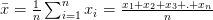Unterschied zwischen Mittelwert und Mittelwert (Mittelwert): Median vs Mittelwert (Mittelwert)

Median vs Durchschnitt (Mittelwert)

Mittelwert und Mittelwert sind Mittelwerte der zentralen Tendenz in der deskriptiven Statistik. Oft wird das arithmetische Mittel als Durchschnitt einer Menge von Beobachtungen angesehen. Daher wird hier als Durchschnitt angesehen. Der Durchschnitt ist jedoch nicht immer das arithmetische Mittel.

Mittelwert

Der arithmetische Mittelwert ist die Summe der Datenwerte dividiert durch die Anzahl der Datenwerte, d.h. e.

Wenn die Daten aus einem Stichprobenraum stammen, heißt das Stichprobenmittel (

), was eine beschreibende Stichprobenstatistik ist. Obwohl es die am häufigsten verwendete beschreibende Maßnahme für eine Stichprobe ist, ist es keine robuste Statistik. Es ist sehr empfindlich für Ausreißer und Schwingungen.

Betrachten Sie zum Beispiel das Durchschnittseinkommen der Bürger einer bestimmten Stadt. Da alle Datenwerte summiert und dann geteilt werden, wirkt sich das Einkommen einer extrem wohlhabenden Person signifikant auf den Mittelwert aus. Daher sind die Mittelwerte immer eine gute Darstellung der Daten.

Auch im Fall eines Wechselsignals variiert der Strom, der ein Element durchläuft, periodisch von der positiven Richtung zur negativen Richtung und umgekehrt. Wenn wir den durchschnittlichen Strom, der das Element in einer einzigen Periode durchläuft, ausgeben, ergibt dies eine 0, was bedeutet, dass kein Strom durch das Element gelaufen ist, was offensichtlich nicht wahr ist. Daher ist auch in diesem Fall das arithmetische Mittel kein gutes Maß.

Der arithmetische Mittelwert ist ein guter Indikator, wenn die Daten gleichmäßig verteilt sind. Für eine Normalverteilung ist der Mittelwert gleich dem Modus und Median. Es hat auch die niedrigsten Residuen, wenn man den quadratischen Mittelwert des Effektivwerts berücksichtigt; daher die beste beschreibende Maßnahme, wenn ein Datensatz durch eine einzige Nummer dargestellt werden soll.

Mittelwert

Die Werte des mittleren Datenpunkts nach dem Anordnen aller Datenwerte in aufsteigender Reihenfolge sind als Median des Datensatzes definiert.

• Wenn die Anzahl der Beobachtungen (Datenpunkte) ungerade ist, ist der Median die Beobachtung genau in der Mitte der geordneten Liste.

• Wenn die Anzahl der Beobachtungen (Datenpunkte) gerade ist, ist der Median der Mittelwert der beiden mittleren Beobachtungen in der geordneten Liste.

Median teilt die Beobachtung in zwei Gruppen ein; ich. e. eine Gruppe (50%) von Werten höher und eine Gruppe (50%) von Werten niedriger als der Median. Mediane werden speziell in schrägen Verteilungen verwendet und stellen Daten dar, die ziemlich viel besser sind als das arithmetische Mittel.

Median vs Mittelwert (Durchschnitt)

• Mittelwert und Mittelwert sind Mittelwerte der zentralen Tendenz und fassen die Daten zusammen. Der Mittelwert ist unabhängig von der Position der Datenpunkte, aber der Median wird anhand der Position berechnet.

• Der Mittelwert wird stark von Ausreißern beeinflusst, während der Median nicht betroffen ist.

• Daher ist der Median ein besseres Maß als der Mittelwert bei stark verzerrten Verteilungen.

• In den Standard-Normalverteilungen sind Mittelwert und Median gleich.